개발하는 뚱이
🦢선형 회귀란 무엇일까?? (Ei : Ez Ai) 본문
회귀란 무엇일까??
- 통계학에서 회귀란 여러 개의 독립 변수와 한 개의 종속 변수 간의 상관관계를 모델링하는 기법을 통칭합니다.
예를 들어 집값을 예측하는 모델에서 집의 크기, 방의 개수, 화장실 개수 등등은 독립 변수라 할 수 있고 집값은 종속 변수라고 할 수 있습니다. 이제 이러한 관계가 어떠한 식으로 나타나는지 모델링하고 예측하는 방법입니다.
모델링이란 : 주어진 데이터를 수학적 표현(모델)으로 변환하고, 이를 통해 예측 또는 분석을 할 수 있는 구조를 만드는 과정
쉽게 정리 하자면 두 변수 사이의 상관관계를 분석하는 방법이라고 생각하면 쉽습니다.
그렇다면 이제 회귀 방법 중에서도 가장 기본적인 형태인 선형 회귀에 대해 설명을 해보겠습니다.
선형 회귀란??
선형 회귀는 어떠한 독립 변수와 종속 변수간의 관계를 예측할 때, 그 사이를 직선이라 가정한 후 모델링하는 지도 학습의 알고리즘 중 하나입니다.(y = ax + b)
쉽게 말해서 독립 변수와 종속 변수 사이의 관계가 직선으로 표현될 수 있다고 가정하는 방법을 말하는 것 입니다.
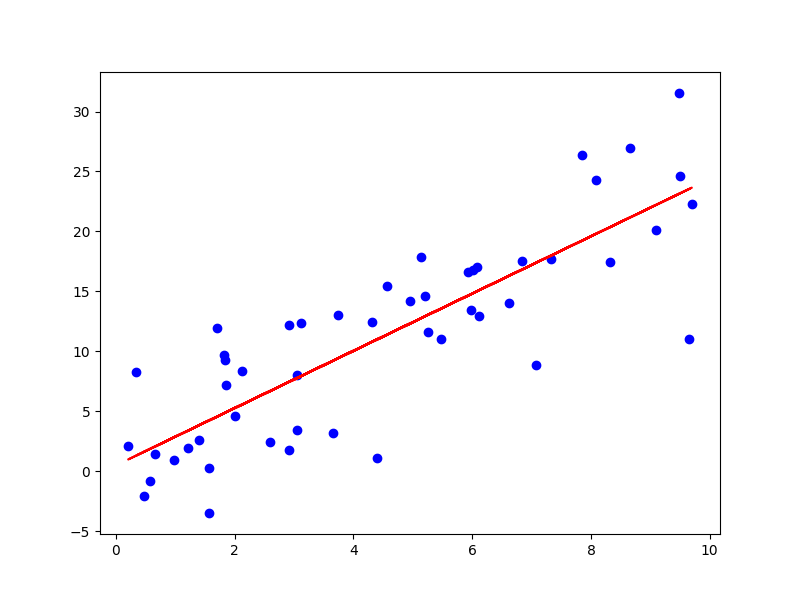
이 그림은 선형 회귀를 나타낸 그림입니다.
여러 점 중 가장 적절한 선을 찾을 것을 확인할 수 있는데, 과연 인공지능은 어떻게 이 적절 선을 어떻게 찾을 수 있었을까요??
(레벨 업) 선형 회귀가 올바른 직선을 찾는 방법

선형 함수는 y = ax+b라는 형태로 표현됩니다. (여기서 a는 기울기고 b는 y의 절편입니다.)
이제 각 데이터의 대해 실제 값 y와 예측값 y^ 사이를 잔차라고 부르며 이 잔차를 줄이는 것이 목표입니다. 이 잔차를 줄이기 위해 잔차의 곱을 최소화하는 최소제곱법(OLS)을 사용합니다.
그렇게 하여금, a와 절편 b를 구하여 가장 적합한 직선을 찾게 되는 것 입니다.
잔차의 곱을 최소화 한다는 것은 잔차의 제곱합이 가장 작은 직선을 찾는 방법을 이야기 하고
잔차를 제곱하는 이유는 양수를 만들기 위해서, 큰 오차를 강조하기 위해서, 미분이 가능해서 이다.
간단요약
- 회귀는 두 변수 사이의 상관관계를 분석하는 방법
- 선형 회귀는 독립 변수와 종속 변수 사이의 관계가 직선으로 표현될 수 있다고 가정하는 방법
- 실제값과 예측값의 잔차를 줄이기 위해 최소제곱법을 활용하여 가장 적합한 선을 찾음
선형 회귀 코드 구현
코드를 읽어 보면서 흐름을 아는것이 중요합니다.
이해가 안 되더라도 한 번씩 읽어보는것을 권장합니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 데이터 생성 및 변환
x = np.array([1, 2, 3, 4, 5]).reshape(-1, 1) # 2차원 데이터로 변환
y = np.array([2, 4, 5, 4, 5])
test_x = np.array([6, 7, 8]).reshape(-1, 1) # 예측을 위한 새로운 데이터
# 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(x, y)
# 기울기a와 절편 b 출력
a = model.coef_[0]
b = model.intercept_
print(f"기울기 a: {a}, 절편 b: {b}")
# 예측값 계산
y_pred = model.predict(test_x)
# 결과 시각화
plt.scatter(x, y, color="blue", label="Data points") # 실제 데이터
plt.scatter(test_x, y_pred, color="green", label="Predicted points") # 예측된 값들을 점으로 표시
plt.plot(np.concatenate((x, test_x)), model.predict(np.concatenate((x, test_x))), color="red", label="Regression line") # 회귀 직선
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()
언제나 배우며 성장하는 학생입니다.
정리한 것 중 잘못된 거나 추가 사항이 있으시다면 피드백을 남겨주시면 정말 감사하겠습니다.
이메일 : hyohyeonkim08@gmail.com
'Ei(Ez Ai)' 카테고리의 다른 글
| 🦕SVM이란??(Ei : Ez Ai) (0) | 2024.11.17 |
|---|---|
| 💣릿지 & 라쏘 회귀란??(Ei : Ez Ai) (4) | 2024.11.02 |
| 🛬손실함수와 경사하강법이란??(Ei : Ez Ai) (2) | 2024.10.20 |
| 🌲의사결정 트리란??(Ei : Ez Ai) (6) | 2024.10.05 |
| 🐍로지스틱 회귀란 무엇일까?? (Ei : Ez Ai) (2) | 2024.10.02 |




