개발하는 뚱이
🛬손실함수와 경사하강법이란??(Ei : Ez Ai) 본문
손실함수란??
손실함수란 실제값과 예측값의 차이를 나타내는 말입니다.
손실함수는 모델이 어떠한 방향으로 학습을 해야 하는지 알려줍니다.(나침반과 같은 역할을 함)
과연 어떻게 손실함수를 구할까??
손실함수도 손실은 구하는 방법이 여러 가지가지 있습니다.
대표적으로 MSE, MAE에 대해 소개하겠습니다.
MSE(Mean Squared Error)
- 평균 제곱 오차로 실제값과 예측값을 뺀 뒤 제곱하고 평균을 내어 손실함수를 구합니다.
- 오차에 대해 민감한 특징을 가지고 있습니다.
(데이터 개수 : n, 실제값 : yi, 예측값 : y^i)
MAE(Mean Absolute Error)

- 평균 절대 오차로 실제값과 예측값을 뺀뒤 절댓값을 구하고 평균을 내어 손실함수를 구합니다.
- 오차에 대해 MSE보다 덜 민감한 특징을 가지고 있습니다.
그 외에도 Binary Cross-Entropy(이진 분류에서 사용), Categorical Cross-Entropy(다중 분류에서 사용) 등등이 있습니다.
경사하강법이란??
손실함수를 최소값으로 만드는 파라미터(매개변수)를 찾습니다. 이 말은 오차가 낮은 지점을 찾는다는 말입니다.
결국은 함숫값이 가장 낮아지는 방향으로 독립변수의 값을 변형시키며 함숫값이 최솟값이 되는 독립 변수의 값을 탐색하는 방법입니다.
말이 어려울 수도 있는데 쉽게 예시를 들어보겠습니다.
목적지가 산을 내려가는 것이라면 현재 자기 위치에서 경사가 낮은 곳으로 이동하다 보면 산 밑으로 갈 수 있습니다. 이 방법이 경사하강법입니다.
왜 사용해??
손실 함수의 최솟값을 찾아 오차를 줄이기 위해 사용합니다.
?? : 그냥 알잘딱으로 계산 안됨?? --> 엄청 복잡한 형태의 패턴을 가지고 있어서 계산하는데 많은 어려움이 있기 때문에 안됨
경사하강법으로 근삿값을 구하는 과정

x의 값이 증가, 함수의 값이 증가 → x를 음의 방향으로
x의 값이 증가, 함수의 값이 감소 → x를 음의 방향으로
자! 쉽세 이해를 하셨겠죠??
하지만 좋을것 같은 경사하강법도 문제점이 존재합니다.
경사하강법의 문제점
1. 과도하게 step-size를 설정한 경우

함수의 최소값을 계산하기 어려워질 수 있습니다. 또한 함수의 값이 커지는 방향으로 최적화될 수 있습니다.
2. 너무 작게 step size를 설정한 경우
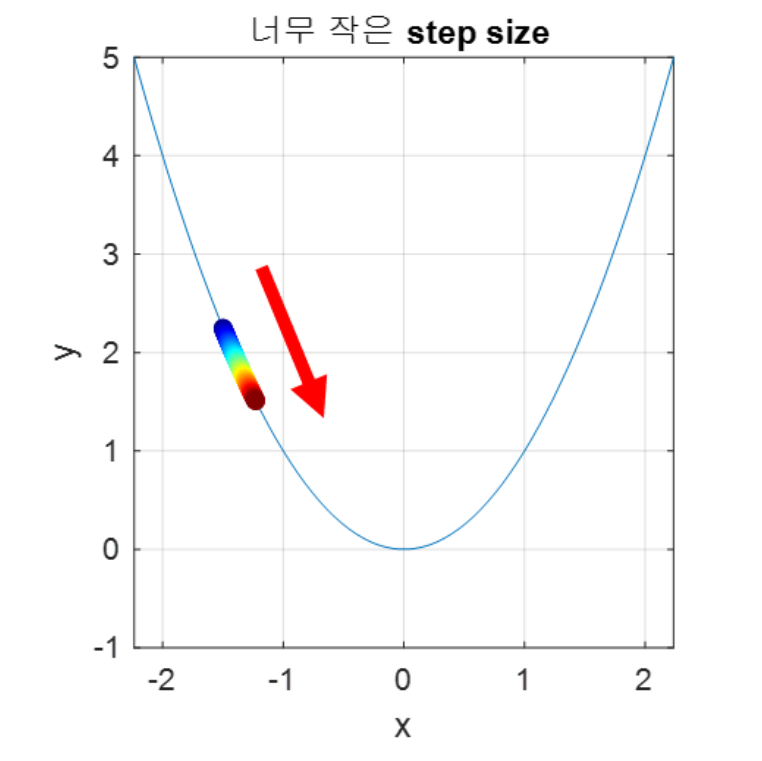
함수의 최솟값을 찾는데 너무 많은 시간이 걸립니다.
3. local minima 문제
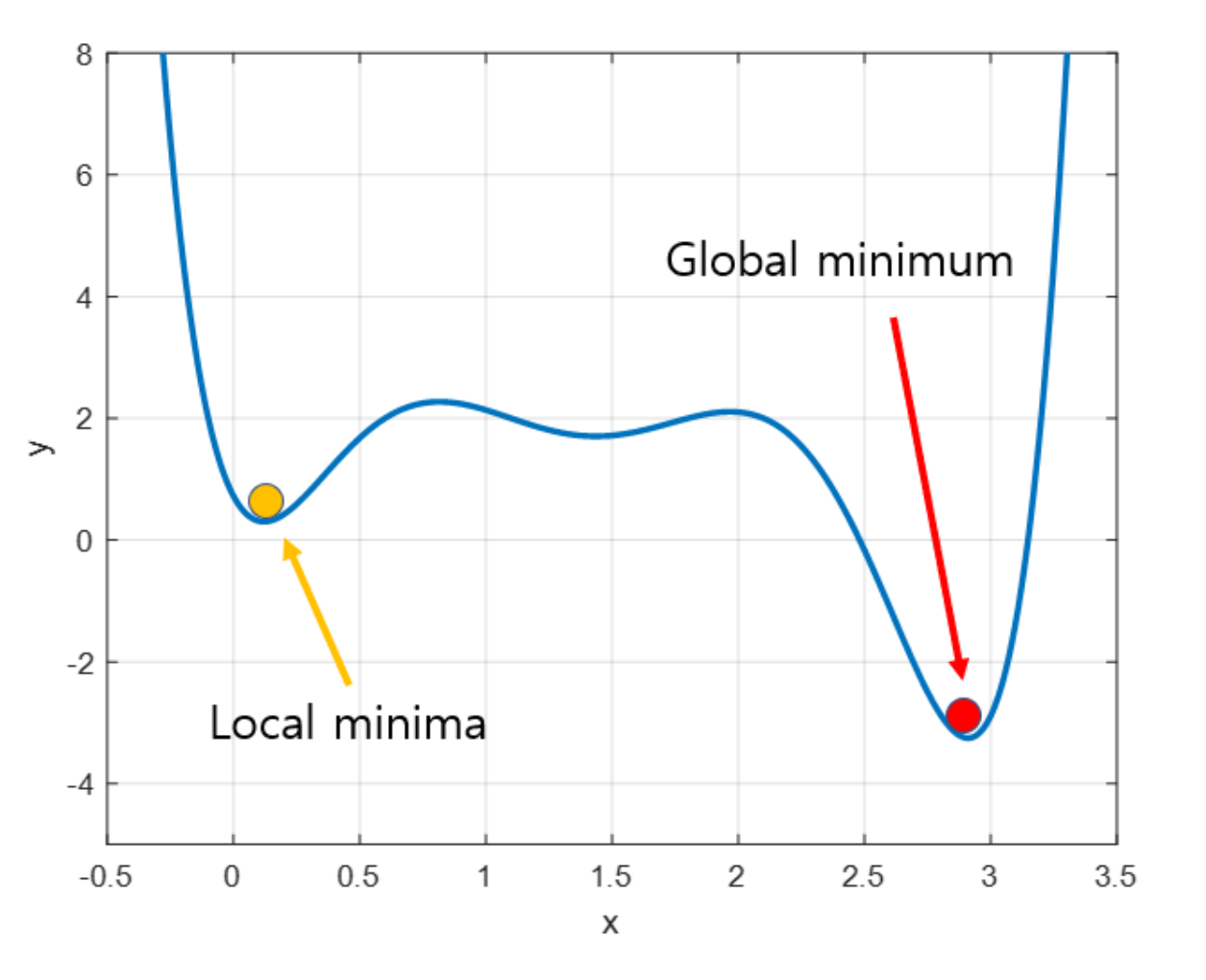
턱이 두개 이상 존재하는데 더 낮은 턱에서 벗어나야 하지만 벗어나지 못하는 문제가 있습니다.
지금 우리는 문제점을 살펴봤습니다. 그러고 난 뒤 저희는 "왜 경사하강법을 사용하지?"라는 의문점이 들 수 있습니다.
그냥 경사하강법은 많은 문제가 될 수 있지만 경사하강법도 확률적 경사하강법, 배치 경사하강법, 미니 배치 경사하강법이 존재 합니다. 이는 Local minima문제를 해결하기위해 도입된 경사하강법 방법입니다. 이번 글에서는 이 3개에 대해 다루지는 않지만 직접 구글링을 통해 배워 알아갔으면 좋겠습니다.
간단 요약
- 손실함수란 실제값과 예측값의 차이(MSE, MAE 등등 방법이 존재)
- 경사하강법은 손실함수를 줄이기 위한 과정
- 경사하강법의 가장 큰 문제는 Local minima문제
(오늘은 코드 없습니다ㅠㅠ)
언제나 배우며 성장하는 학생입니다.
정리한 것 중 잘못된 거나 추가 사항이 있으시다면 피드백을 남겨주시면 정말 감사하겠습니다.
이메일 : hyohyeonkim08@gmail.com
'Ei(Ez Ai)' 카테고리의 다른 글
| 🦕SVM이란??(Ei : Ez Ai) (0) | 2024.11.17 |
|---|---|
| 💣릿지 & 라쏘 회귀란??(Ei : Ez Ai) (4) | 2024.11.02 |
| 🌲의사결정 트리란??(Ei : Ez Ai) (6) | 2024.10.05 |
| 🐍로지스틱 회귀란 무엇일까?? (Ei : Ez Ai) (2) | 2024.10.02 |
| 🦢선형 회귀란 무엇일까?? (Ei : Ez Ai) (2) | 2024.09.23 |





